Sufficient Causes

A walkthrough of Pearl. J Causal Infer 2019; 20190026.

This paper considers the example of Oxygen, Matches, and Fire in The Book of Why:

“A fire broke out after someone struck a match, and the question is ‘What caused the fire, striking the match or the presence of oxygen in the room?’ Note that both factors are equally necessary, since the fire would not have occurred absent one of them. So, from a purely logical point of view, the two factors are equally responsible for the fire. Why, then, do we consider lighting the match a more reasonable explanation of the fire than the presence of oxygen”

Pearl then introduces the idea of sufficiency: that striking a match is much more likely to be a sufficient condition for the fire than the presence of oxygen.

Let F denote the presence (F=1) or absence (F=1) of a fire, and let M denote whether a match was struck (M=1) or not (M=0). The probability that the match was a sufficient condition can be represented as

SufficientCauses_1.png

Here, F[M=1]=1 denotes a counterfactual. That is, the event that F=1 had only M=1. Note, however, that this probability is conditioned on observing a situation where the match was not struck. Thus, Eq. 1 quantifies the probability that a fire would occur had a match instead been struck.

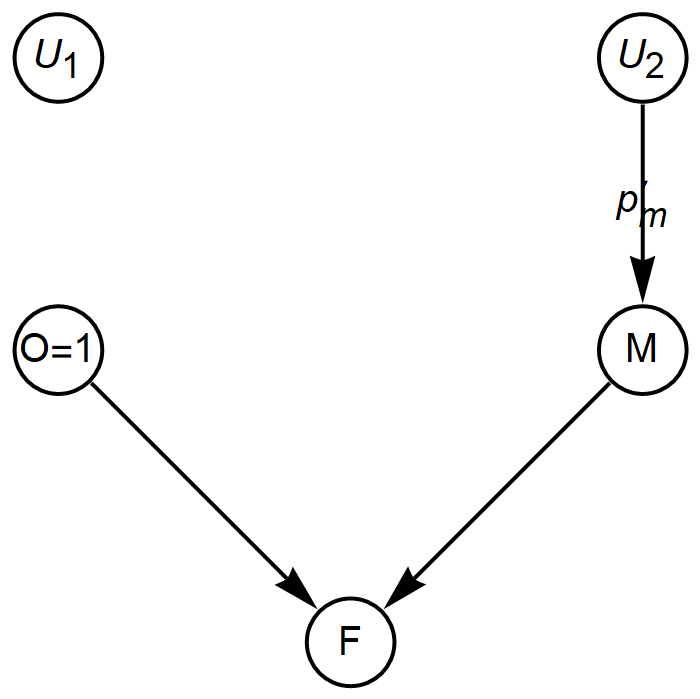
Now let O be the condition that oxygen is present (O=1) or not (O=0).

Pearl constructs the following graphical model for the situation:

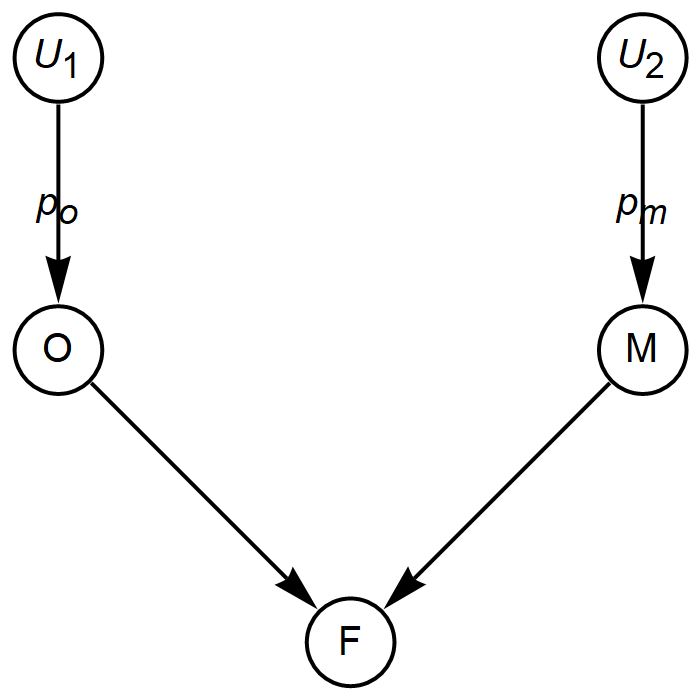
SufficientCauses_2.gif

Above, the SufficientCauses_3.png and SufficientCauses_4.png nodes are noise that generate random variables M and O with probabilities SufficientCauses_5.png and SufficientCauses_6.png, respectively, where SufficientCauses_7.png. These distributions are Bernoulli:

SufficientCauses_8.gif

We have that F=SufficientCauses_9.png, where SufficientCauses_10.png is Kronecker’s delta. The joint distribution over M ∧ O is as follows:

SufficientCauses_11.png

The consequent probability distribution over F is

SufficientCauses_12.png

Computing the Probability of Sufficiency

Pearl describes a three step procedure for making this counterfactual claim.

1. Abduction: “Updating history in light of available evidence”
2. Action: “Bending the course of history (minimally) to comply with the antecedent”
3. Prediction: “Predicting the outcome based on the updated past and modified model”.

He sets out to compute the following quantities:

SufficientCauses_13.png

SufficientCauses_14.png

Step 1. Abduction

Note that in both cases of Eqs. 2 and 3, we have that F=0. We need to therefore adjust the probabilities of M and O to account only for the situation in which we did not observe a fire.

Pearl does this using Bayes’ rule.

SufficientCauses_15.png

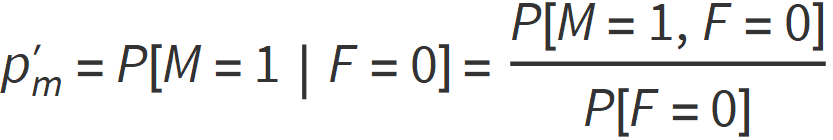
SufficientCauses_16.png

Note that P[O=1, F=0] is equivalent to P[O=1, M=0].

SufficientCauses_17.png

SufficientCauses_18.png

SufficientCauses_19.png

SufficientCauses_20.png

We can now update the graphical model with these new probabilities:

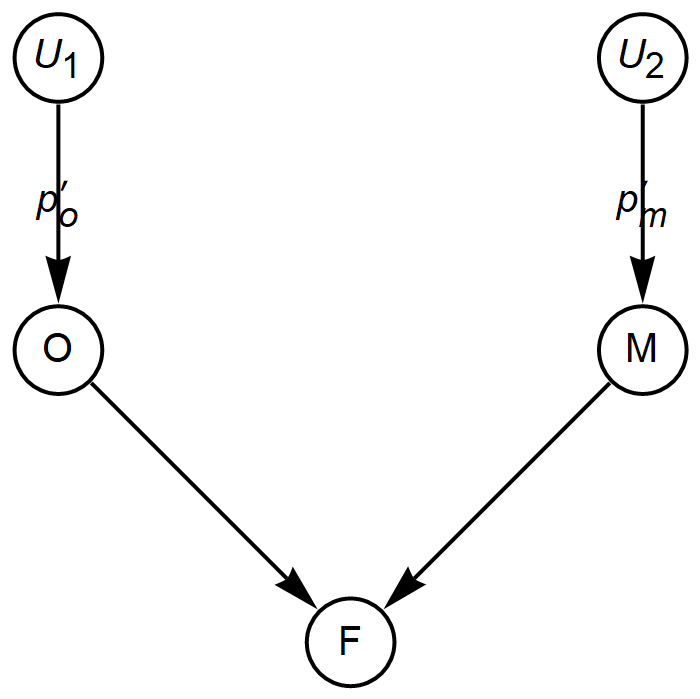
SufficientCauses_21.gif

SufficientCauses_22.gif

The updated joint distribution is therefore as follows:

SufficientCauses_23.png

Step 2: Action

In this stage, we compute PS[M] and PS[O] by taking the new priors SufficientCauses_24.png and SufficientCauses_25.png, and “simulate the action do[M=1]” (in Pearl’s words from the paper). Graphically, this corresponds to the following models.

Model SufficientCauses_26.png is

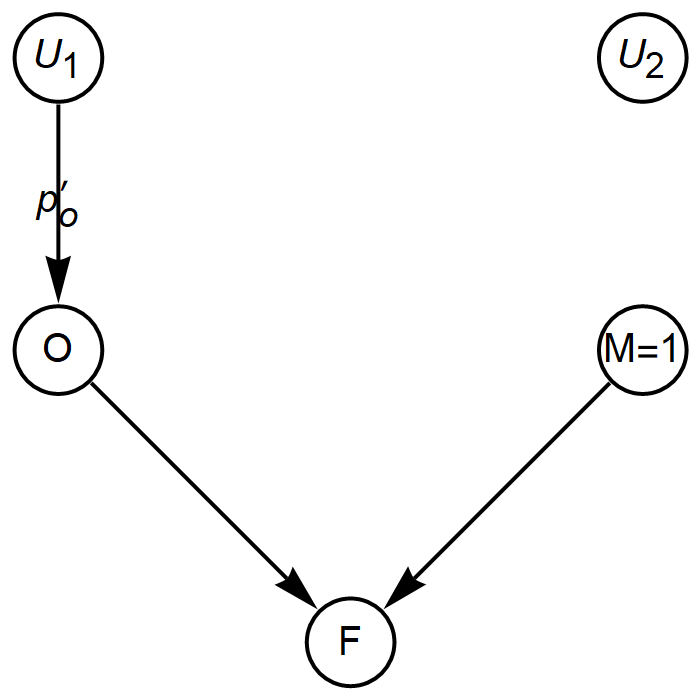
SufficientCauses_27.gif

and model SufficientCauses_28.png is as follows:

SufficientCauses_29.gif

Step 3: Prediction

Now, we have to simply compute P[F=1] under SufficientCauses_30.png and SufficientCauses_31.png, respectively.

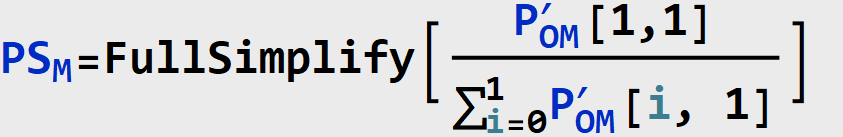
SufficientCauses_32.png

SufficientCauses_33.png

Note that SufficientCauses_34.png:

SufficientCauses_35.png

SufficientCauses_36.png

Note that SufficientCauses_37.png:

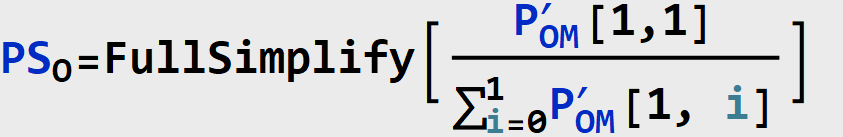
SufficientCauses_38.png

SufficientCauses_39.png

SufficientCauses_40.png

SufficientCauses_41.png

So, is the Match a Better Explanation for the Fire?

We can now answer the question of whether a match being lit is a better explanation for the fire than is the presence of oxygen. Namely, the match is a better explanation if its probability of sufficiency PS[M] is greater than that of the oxygen PS[O].

SufficientCauses_42.png

SufficientCauses_43.png

SufficientCauses_44.png

SufficientCauses_45.png

Created with the Wolfram Language