Schur-Concavity of Rényi Heterogeneity

Abraham Nunes MD PhD MBA
Dalhousie University, Halifax, Nova Scotia, Canada

The Rényi heterogeneity of system X defined on state space X={1,2,..., n}, with probability distribution RenyiSchur_1.png is

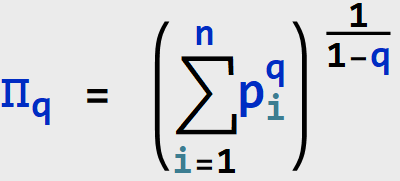
RenyiSchur_2.png

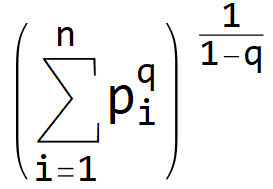
RenyiSchur_3.png

RenyiSchur_4.png

RenyiSchur_5.png

The Schur-Ostrowski criterion states that if f is a symmetric function and all first partial derivatives exist, then f is Schur-concave iff

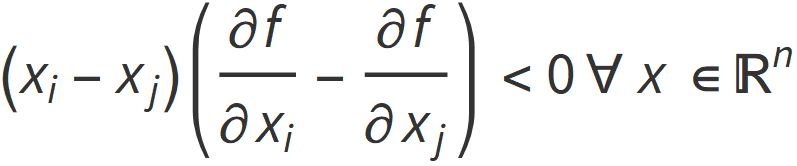
RenyiSchur_6.png

holds for all 1≤i≠j<n

PROPOSITION 1 (Symmetry of Rényi Heterogeneity). Given a probability vector RenyiSchur_7.png and permutation function RenyiSchur_8.png, the Rényi heterogeneity

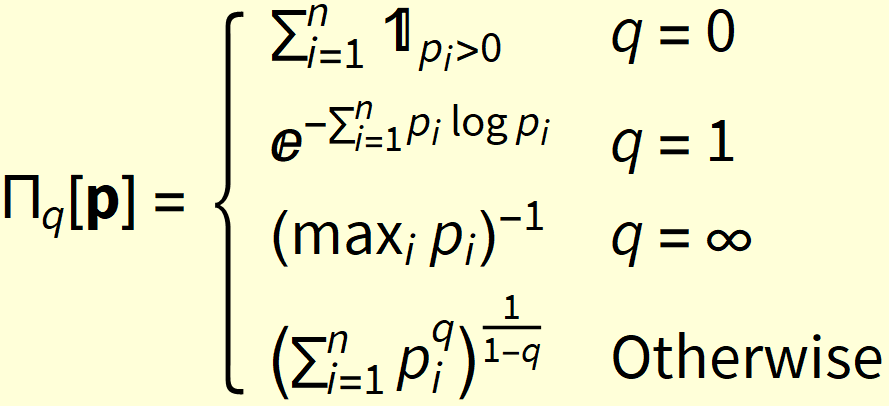    RenyiSchur_9.png,

satisfies

    RenyiSchur_10.png.

The proof trivially follows from the commutativity of addition.

PROPOSITION 2 (Differentiability). Given a probability vector RenyiSchur_11.png and the Rényi heterogeneity

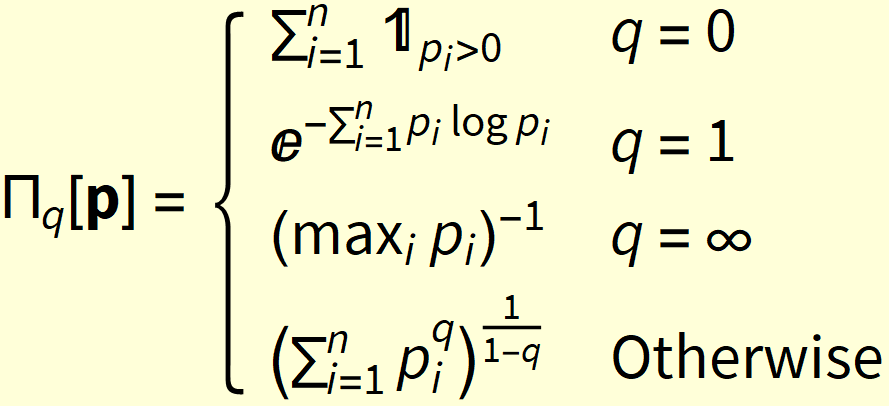    RenyiSchur_12.png,

we have that ∃ RenyiSchur_13.png RenyiSchur_14.png.

Proof.  At q∉{0,1,∞}, we have

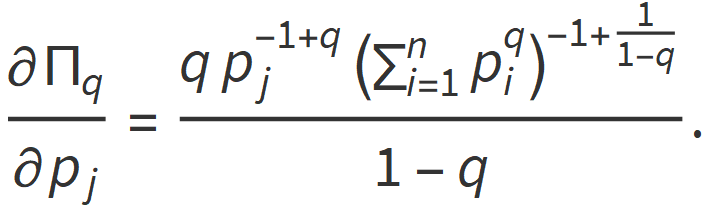
RenyiSchur_15.png

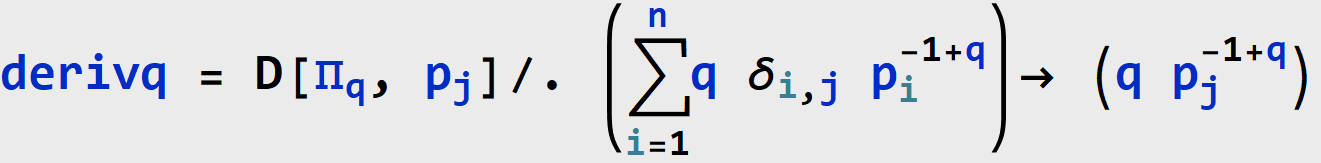
RenyiSchur_16.png

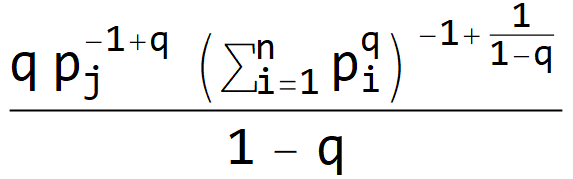
RenyiSchur_17.png

At q=0, we have

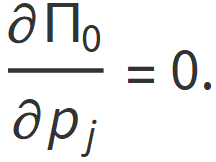
RenyiSchur_18.png

RenyiSchur_19.png

RenyiSchur_20.png

At q=1 we have

RenyiSchur_21.png

RenyiSchur_22.png

RenyiSchur_23.png

At q=∞ we have

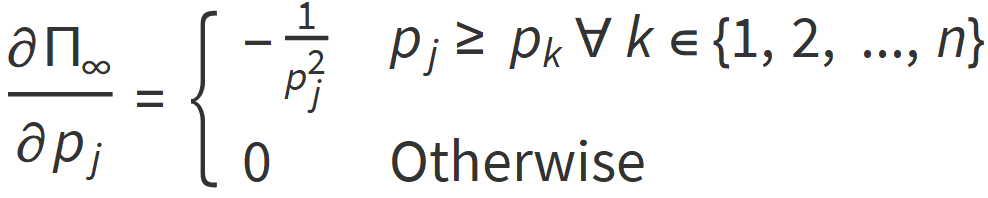
RenyiSchur_24.png

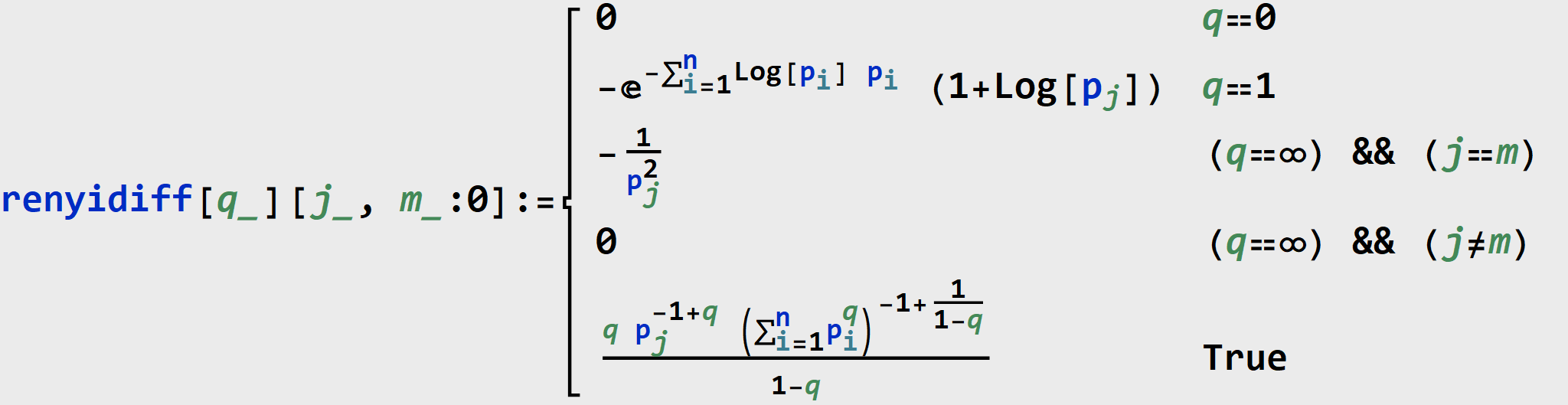
RenyiSchur_25.png

THEOREM (Schur-Concavity of Rényi Heterogeneity). The Rényi heterogeneity is Schur-concave.

Proof.

RenyiSchur_26.png

RenyiSchur_27.png

RenyiSchur_28.png

RenyiSchur_29.png

RenyiSchur_30.png

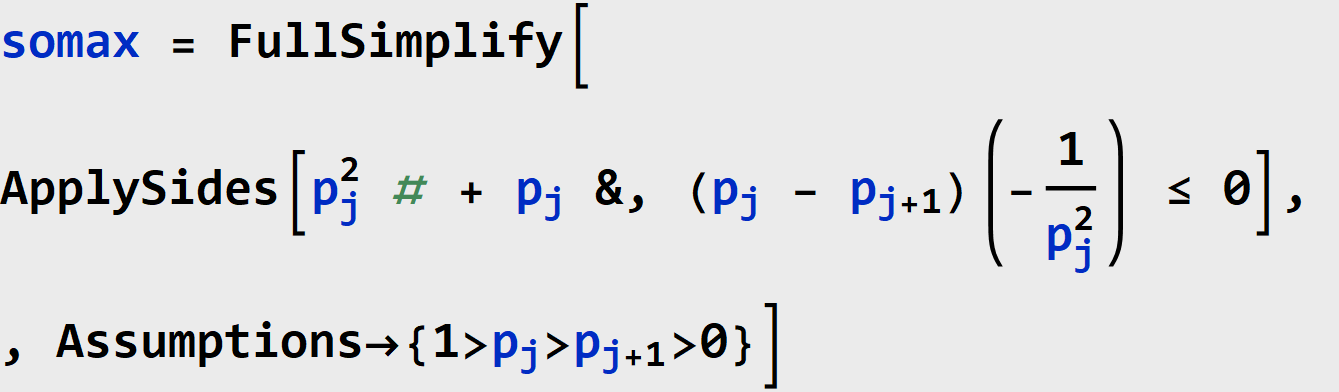
RenyiSchur_31.png

RenyiSchur_32.png

RenyiSchur_33.png

RenyiSchur_34.png

RenyiSchur_35.png

RenyiSchur_36.png

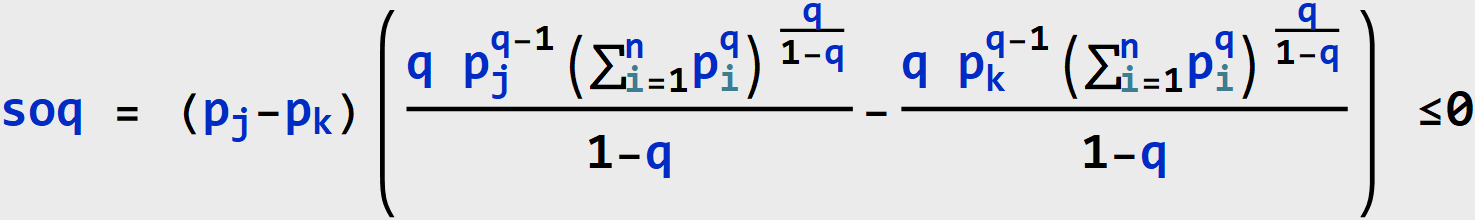
RenyiSchur_37.png

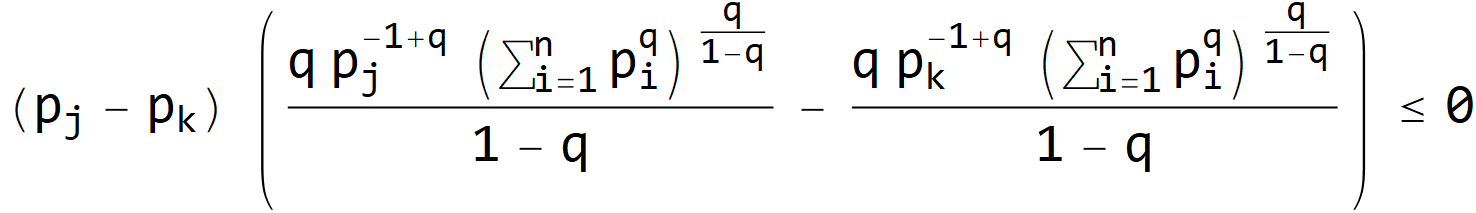
RenyiSchur_38.png

RenyiSchur_39.png

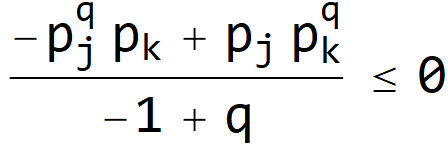
RenyiSchur_40.png

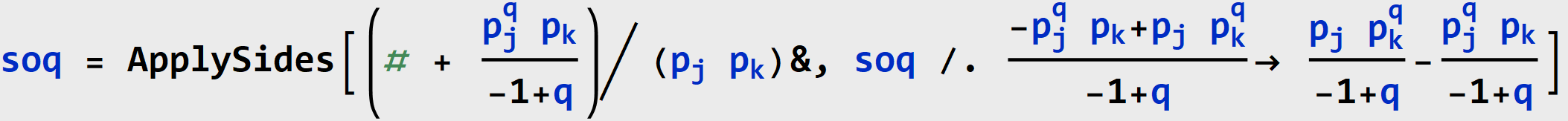
RenyiSchur_41.png

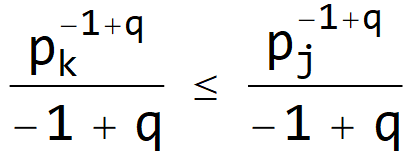
RenyiSchur_42.png

RenyiSchur_43.png

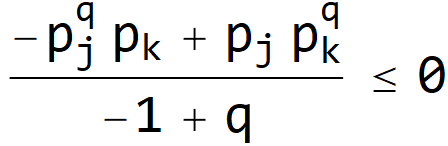
RenyiSchur_44.png

RenyiSchur_45.png

Created with the Wolfram Language